
The product of an m × n m\times n m × n m, times, n matrix and an n × k n\times k n × k n, times, k matrix is an m × k m\times k m × k m, times, k matrix. O A = O O A=O O A = O O, A, equals, O and A O = O AO=O A O = O A, O, equals, O I A = A IA=A I A = A I, A, equals, A and A I = A AI=A A I = A A, I, equals, A Using row operations, convert the left-hand half of the double-wide in the identity matrix.
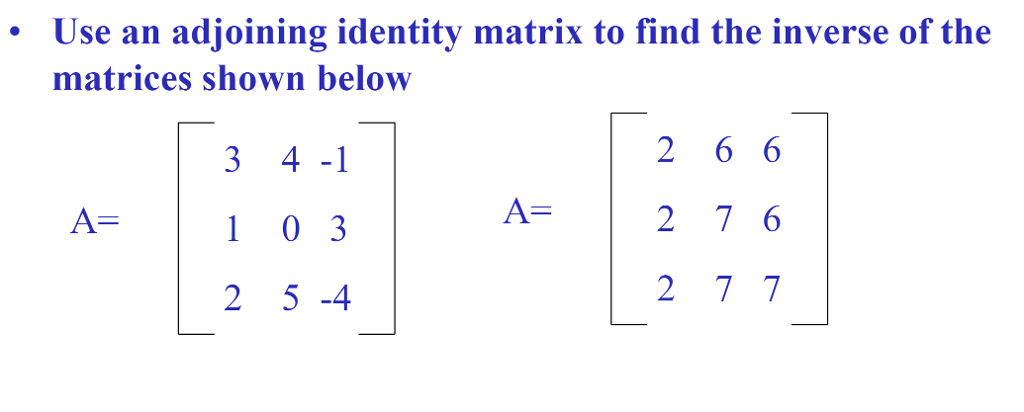
Identity matrices are used in factor analysis solutions and matrix. Append to this matrix the identity matrix, making one matrix that is now twice as wide as it is tall. (symbol: I) a square matrix with values of 1 along its main diagonal and 0s elsewhere. ( B + C ) A = B A + C A (B+C)A=BA+CA ( B + C ) A = B A + C A left parenthesis, B, plus, C, right parenthesis, A, equals, B, A, plus, C, A To find the inverse of a matrix, follow these steps: Write out the matrix that youre wanting to invert.
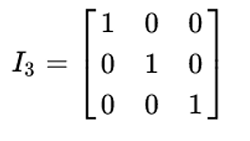
( A B ) C = A ( B C ) (AB)C=A(BC) ( A B ) C = A ( B C ) left parenthesis, A, B, right parenthesis, C, equals, A, left parenthesis, B, C, right parenthesisĪ ( B + C ) = A B + A C A(B+C)=AB+AC A ( B + C ) = A B + A C A, left parenthesis, B, plus, C, right parenthesis, equals, A, B, plus, A, C The commutative property of multiplication does not hold! \small does not hold! start color #df0030, start text, d, o, e, s, space, n, o, t, space, h, o, l, d, !, end text, end color #df0030Ī B ≠ B A AB\neq BA A B = B A A, B, does not equal, B, A glm::mat4 constructor that takes only a single value constructs a diagonal matrix: glm::mat4 m4( 1.0f ) // construct identity matrix.


 0 kommentar(er)
0 kommentar(er)
